背景
近年来,矢量化方法(vectorized approaches)因其能够捕捉交通场景中复杂的交互作用,在运动预测领域占据了主导地位。然而,现有方法忽略了问题的对称性,并面临着高昂的计算成本,因此在不牺牲预测性能的前提下,实现实时多智能体运动预测仍然面临挑战。
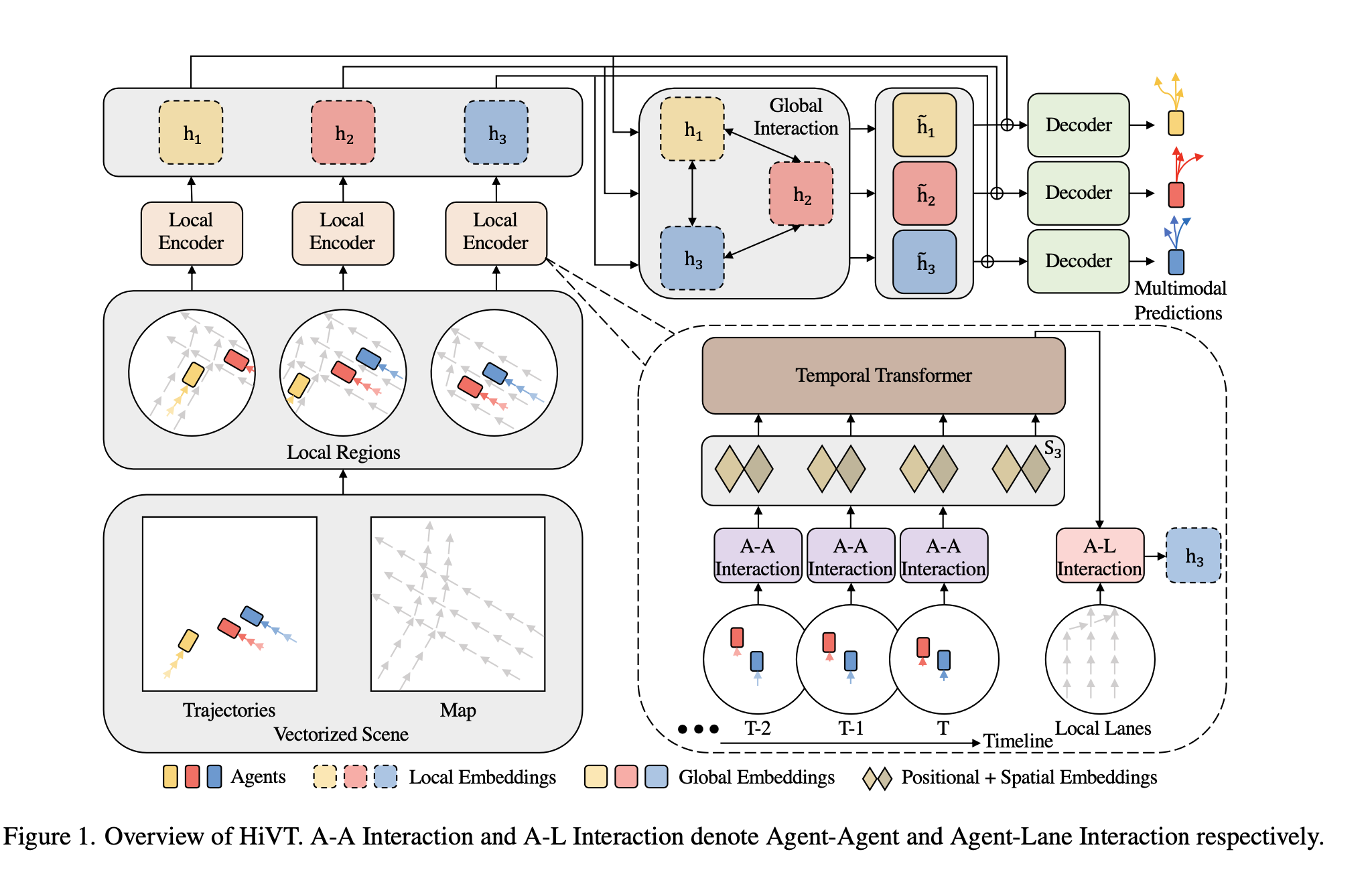
通过将问题分解为局部上下文提取和全局交互建模,我们的方法能够高效地对场景中大量的智能体(agents)进行建模。同时,我们提出了一种平移不变的场景表示(translation-invariant scene representation)和旋转不变的空间学习模块(rotation-invariant spatial learning modules),它们能够提取对场景的几何变换具有鲁棒性的特征,并使模型能够在单次前向传播中对多个智能体做出准确的预测。
-
场景(智能体和地图)被表示为矢量化实体的集合(智能体的轨迹段和地图中的车道段) 。
-
与其他方法不同,几何属性使用相对位置 。例如,智能体 i 的轨迹表示为${p_i^t - p_i^{t-1} }_{t=1}^T$。车道段 ξ 由 $p^ξ_1−p^ξ_0$ 定义 。
-
这种表示方法自然保证了平移不变性 。
-
为了保留空间关系,引入了智能体对之间和智能体-车道对之间的相对位置矢量(例如,pjt−pit 表示智能体 j 相对于智能体 i 的位置)
-
分层矢量变换器 (Hierarchical Vector Transformer):
-
该模型分解了空间和时间维度,仅在每个时间步局部学习空间关系 。
-
空间被划分为 N 个局部区域,每个局部区域以一个智能体为中心 。
- 局部编码器 (Local Encoder):
- note: On the other hand, the computational complexity is reduced from O((NT + L)2) to O(NT2 + TN2 + NL) by the factorization of the space and the time dimensions and is further reduced to O(NT2 + TNk+ Nℓ) by limiting the radius of the local regions, where k<N and ℓ<L. (减少复杂度而实现这些交互)
- 智能体-智能体交互 (Agent-Agent Interaction): 对于每个局部区域和每个时间步,对中心智能体和相邻智能体之间的关系进行建模 。使用了一个旋转不变的交叉注意力模块 。局部矢量根据中心智能体最新轨迹段的方向 (θi) 进行旋转,然后由 MLP 处理以获得嵌入 (zit,zijt) 。这些嵌入用于计算注意力的查询 (query)、键 (key) 和值 (value) 矢量 。注意力模块中使用门控函数 (gating function) 来融合环境特征和中心智能体的特征 。(R这边是旋转的意思,ai代表agent i的语义信息)
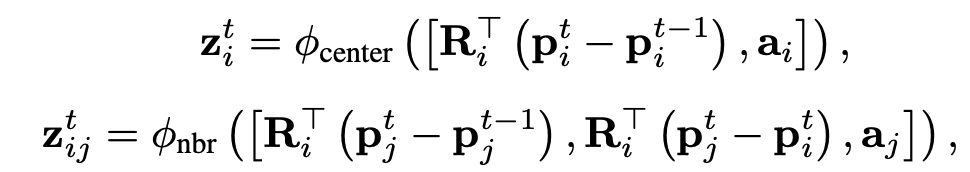
-
时间依赖性 (Temporal Dependency): 一个时间 Transformer 编码器处理每个中心智能体的空间嵌入序列 ${s_{i}}_{i=1}^t$ 。添加了一个额外的可学习标记 (token) 和位置嵌入 。应用时间掩码,使标记只关注先前的时间步 。
- 智能体-车道交互 (Agent-Lane Interaction): 融合局部地图信息 。局部车道段和智能体-车道相对位置矢量在当前时间步 T 被旋转,然后由一个 MLP 编码 。使用中心智能体的时空特征作为查询,编码后的车道段特征作为键/值来计算注意力 。这产生了最终的局部嵌入 hi 。
-
全局交互模块 (Global Interaction Module):
-
聚合不同智能体的局部上下文,以捕捉场景中的远程依赖关系和场景级动态 。
- 一个 Transformer 编码器能够感知局部坐标系之间的差异(例如,pjT−piT 和 Δθij=θj−θi) 。这些差异被嵌入 (eij) 并整合到用于全局空间注意力的矢量转换中 。这产生了全局表示 h~i 。
-
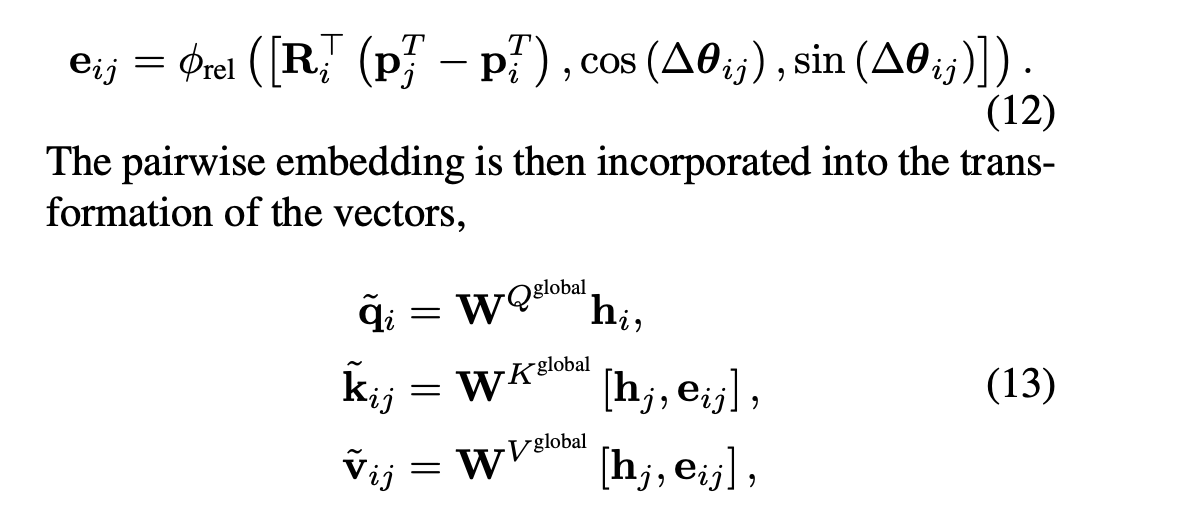 - 获取一个坐标相对于另外一个坐标的位置和角度
-
-
多模态未来解码器 (Multimodal Future Decoder):
-
将未来轨迹的分布参数化为一个混合模型,其中每个混合成分是一个拉普拉斯分布 。
-
一个 MLP 接收局部 (hi) 和全局 (h~i) 表示作为输入,并为每个智能体 i、混合成分 f 和未来时间步 t 在局部坐标系中输出位置 μi,ft 及其相关的不确定性 bi,ft 。
-
另一个 MLP 产生混合系数 。
-
-
-
训练 (Training):
-
采用“多样性损失” (variety loss),它在训练期间只优化 F 个预测中最好的一个 。
-
最终的损失函数包括回归损失 (Lreg) 和分类损失 (Lcls),权重相等 。
-
Lreg 是针对最佳预测轨迹的拉普拉斯分布的负对数似然 。
-
Lcls 是用于优化混合系数的交叉熵损失 。
-
实验
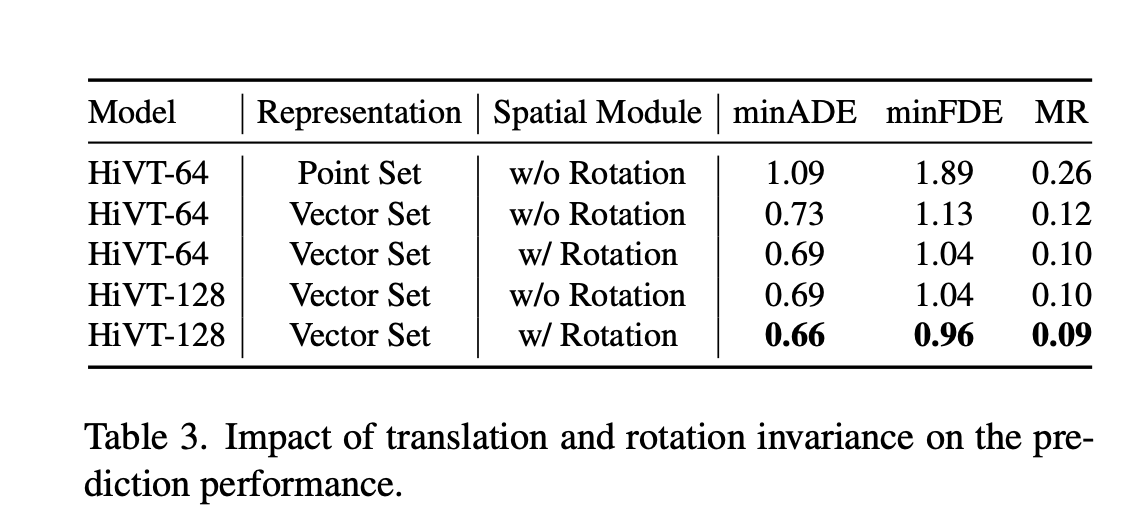
-
Point Set (点集):
- 在这种表示方法中,场景中的实体(如智能体的轨迹点、地图元素等)的几何属性可能涉及到绝对坐标。
- 在 HiVT 论文的消融研究中,当使用 “Point Set” 表示时,他们会将坐标根据自动驾驶车辆在当前时间步的位置和朝向进行归一化 。这种表示是以场景为中心的 (scene-centric),并且对于场景的平移不具有不变性 。
-
Vector Set (矢量集):
- 这是 HiVT 论文中提出的核心场景表示方法。
-
在这种表示方法中,所有矢量化实体的几何属性都用相对位置来描述,避免使用任何绝对坐标 。
-
例如,智能体 i 的轨迹被表示为相邻时间步之间的位移矢量${p_i^t - p_i^{t-1} }_{t=1}^T$ 。车道段的几何属性由其起点到终点的矢量 $p^ξ_1−p^ξ_0$ 给出 。
- 这种表示方法将场景转换为一个完全由矢量组成的集合,从而自然地保证了平移不变性 (translation invariance) 。
 看起来时间约束对实验影响巨大
看起来时间约束对实验影响巨大