Latent variable sequential set transformersfor joint multi Agent motion prediction（特点：推理和训练很快）

Posted on May 20, 2025

AutoBot 是一种用于预测多智能体未来轨迹的生成式模型，它结合了：

  • Set Transformers：处理集合结构（如不定数量的代理人）。

  • Sequential Modeling：处理时间序列依赖。

  • Latent Variables：使用 离散隐变量 捕捉多模态未来。

  • Transformer Encoder-Decoder 架构：整合社交（代理人间）和时间维度。

从图中可以看到输入是agents* time，代表每个agent各个时间步的信息，

架构

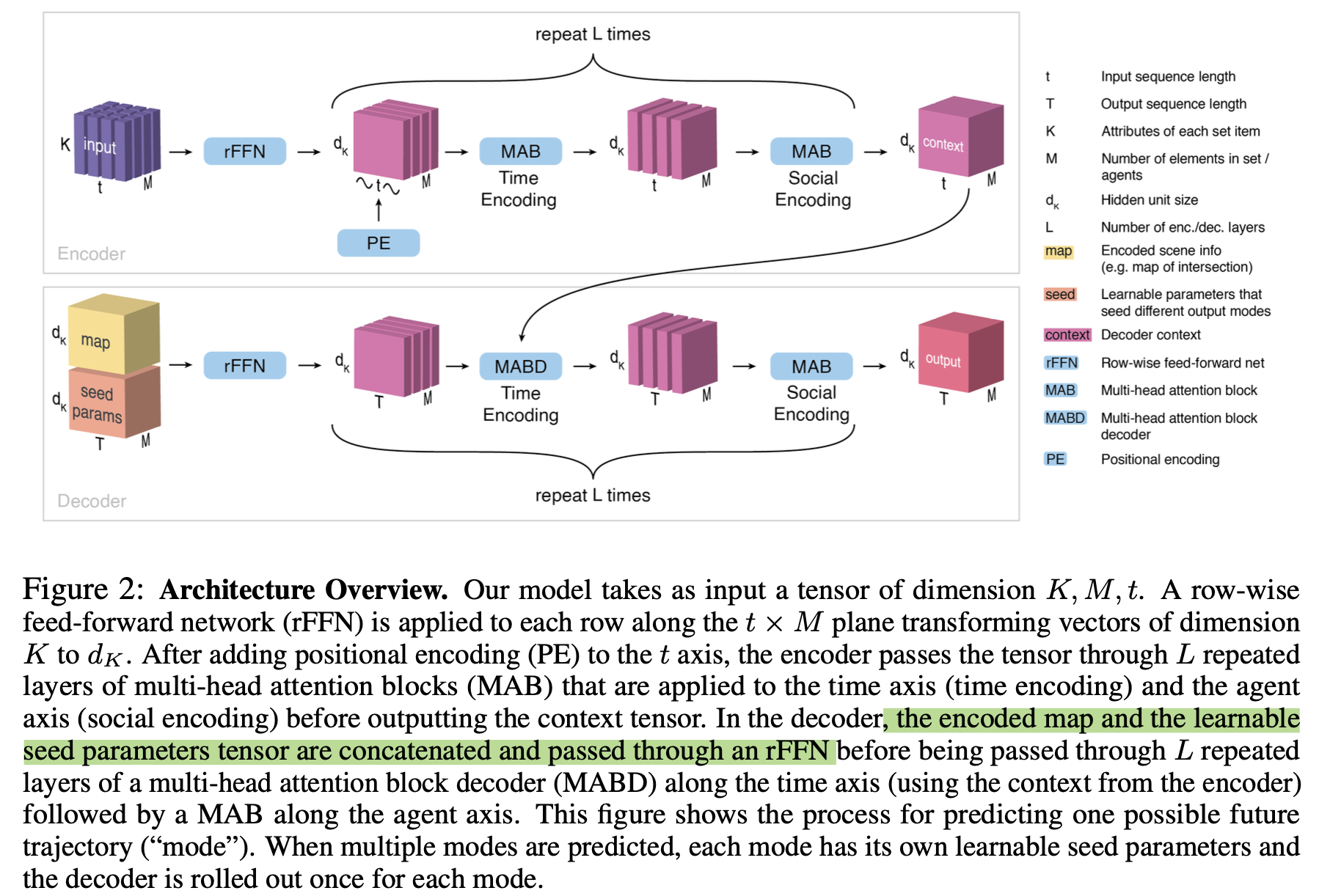
1. Encoder（时序-社交特征编码）

Step 1：行向嵌入（Row-wise FFN）

  • 每个 agent 在每个 timestep 的 K维向量通过一个前馈网络嵌入到隐藏空间维度$d_K$​。

Step 2：时间轴处理（Temporal Attention）

  • 将所有 agent 的历史轨迹视为独立时间序列，使用 MHSA 对时间维进行注意力建模。

Step 3：社会轴处理（Social Attention）

  • 在每个 timestep 上，对所有 agent 进行注意力建模，获取 agent 间交互信息。

Step 4：交替叠加

  • Temporal + Social MHSA 操作交替叠加 $L_{enc}$​ 层，输出上下文张量：
    $C \in \mathbb{R}^{d_K \times M \times t}$
  • 具备 permutation equivariance（排列等变性）对 agent 顺序不敏感

  • 2. Decoder（多模态轨迹生成）

    Step 1：构造 seed 参数

  • 为每个潜在模式 $Z_i$​，定义 使用 c组 learnable seed 参数 $Q_i \in \mathbb{R}^{d_K \times T}$，代表不同未来模式

  • 将其 复制 M 次 得到 $Q’_i \in \mathbb{R}^{d_K \times M \times T}$。

NOTE:使得模型推理和训练快是因为$Q_i$($Q_i \in R(dk ,T )$ ,where $i \in {1, …, c}$) 一一对应一个离散隐变量 其次，它们通过允许AutoBot在不进行序列采样的情况下，仅通过解码器的一次前向传播（single forward pass）即可对整个场景进行推理，从而提高了AutoBot的速度。先前的工作（例如，Tang and Salakhutdinov (2019)）使用具有交错社交注意力（interlaced social attention）的自回归采样（auto-regressive sampling）来预测未来场景，这使得能够实现具有社交一致性的多智能体预测。其他工作（例如，Messaoud et al. (2020)）采用单输出多层感知机（single output MLP）通过一次前向传播来独立生成每个智能体的整个未来轨迹。AutoBot利用Transformer的注意力机制，通过从每个种子参数矩阵（seed parameter matrix）确定性地解码未来场景，结合了这两种方法的优点。在附录C.5中，我们将AutoBot的推理速度与其自回归对应方法进行了比较。

  • 自回归（autoregressive）模型：

    • 一次生成一个时间步的轨迹；

    • 每一步都 依赖前一步的输出，所以不能并行；

    • 时间复杂度为 O(T)，需循环 T 次；

    • 常用于LSTM、Transformer decoder（如GPT-style decoder）等。

AutoBot 的优化点： AutoBot 用的是：

  • 非自回归（non-autoregressive）解码器

  • 每个隐变量 $Z_i$​ 对应一个 learnable seed $Q_i \in \mathbb{R}^{d_K \times T}$

  • seed 被复制 M 次，形成输入张量 $Q’_i \in \mathbb{R}^{d_K \times M \times T}$

然后：

  • 所有 T 步 + 所有 M 个智能体 一次性送入 Transformer 解码器；

  • 不需要像 RNN 那样逐步采样；

“序列采样”指的是每一步依赖上一时间步输出逐步生成的过程（如RNN/GPT的推理方式）

Step 2：融合环境信息

  • 从地图图像提取环境向量 $m_i$(CNN提取），广播为张量 $M_i \in \mathbb{R}^{d_K \times M \times T}$；
  • 与 $Q’_i$​ 拼接后通过 rFFN 得到 $H_i$​。

Step 3：两阶段注意力处理

  1. 时间注意力（MABD）：使用 encoder 输出 C 和 decoder输入 $H_i$​，对时间维建模；

  2. 社会注意力（MAB）：在每个 future timestep 对所有智能体做注意力计算。

Step 4：重复 c 次

  • 每个 mode $i \in {1, …, c}$独立生成未来轨迹，输出张量：

    $O \in \mathbb{R}^{d_K \times M \times T \times c}$

  • 最后通过 MLP 投出轨迹坐标或高斯分布参数。

训练目标

使用 显式建模的离散隐变量 Z∈{1,…,c}Z \in {1, \dots, c}Z∈{1,…,c}，通过 最大化似然函数 训练，形式如下：

$\log p_\theta(Y \mid X_{1:t}) = \sum_Z p(Z \mid Y, X_{1:t}) \log p_\theta(Y, Z \mid X_{1:t})$

求梯度 因为 Z 是 离散变量，我们不能像连续变量一样直接用重参数技巧来采样。且后验 $p(Z \mid \mathcal{Y}, \mathbf{X}{1:t})$ 通常依赖于 $\theta$，所以计算会很复杂。 我们用一个易于处理的 近似分布$q(Z) = p{\theta_{\text{old}}}(Z \mid Y, X_{1:t}))$，目标变为：

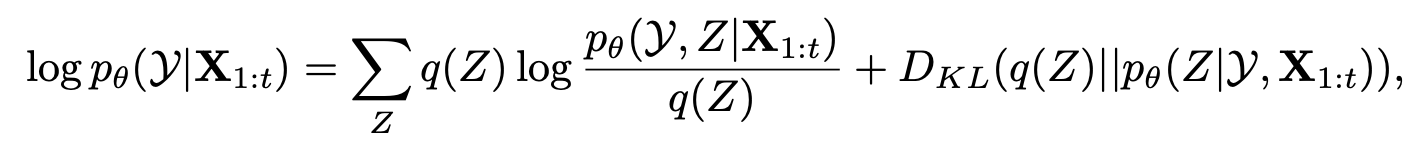
该公式来源于 ELBO（Evidence Lower Bound）分解：

$\log p_\theta(\mathcal{Y} \mid \mathbf{X}{1:t}) = \mathbb{E}{q(Z)}[\log p_\theta(\mathcal{Y}, Z \mid \mathbf{X}{1:t}) - \log q(Z)] + \text{KL}(q(Z) \parallel p(Z \mid \mathcal{Y}, \mathbf{X}{1:t}))$ 我们定义 ELBO 为： $\mathcal{Q}(\theta, q) = \sum_Z q(Z) \log p_\theta(\mathcal{Y}, Z \mid \mathbf{X}_{1:t}) - \sum_Z q(Z) \log q(Z)$ 所以优化目标就变成了最大化下界 $\mathcal{Q}$，并最小化 KL 项。

论文使用了一个聪明的 trick，设定：

$q(Z) = p_{\theta_{\text{old}}}(Z \mid \mathcal{Y}, \mathbf{X}_{1:t})$

即用旧参数生成的模型作为近似分布，这样后验分布可以显式计算，因为 Z 是离散变量，枚举即可。

将联合分布展开：
$p_\theta(\mathcal{Y}, Z \mid \mathbf{X}{1:t}) = p\theta(\mathcal{Y} \mid Z, \mathbf{X}{1:t}) \cdot p\theta(Z \mid \mathbf{X}_{1:t})$

代入 ELBO 得：

$\mathcal{Q}(\theta, \theta_{\text{old}}) = \sum_Z p_{\theta_{\text{old}}}(Z \mid \mathcal{Y}, \mathbf{X}{1:t}) \left[ \log p\theta(\mathcal{Y} \mid Z, \mathbf{X}{1:t}) + \log p\theta(Z \mid \mathbf{X}_{1:t}) \right] \quad \text{(4)}$

同时最小化 KL 散度： $\text{KL}(p_{\theta_{\text{old}}}(Z \mid \mathcal{Y}, \mathbf{X}{1:t}) \parallel p\theta(Z \mid \mathbf{X}_{1:t}))$

此外，为鼓励多样性，引入了 最大熵正则项（mode entropy regularization）：

$L_{\text{ME}} = -\epsilon \max_Z \sum_{\tau=t+1}^{T} H(p_\theta(X_\tau \mid Z, X_{1:t}))$

  • $\mathbb{H}(\cdot)$：是 熵函数，度量概率分布的不确定性；
  • 惩罚那些预测分布不够集中的模式；
  • 鼓励每个离散模式 Z 在输出时保持明确、精确的预测。 综合所有部分，我们的训练目标变成： $\max_\theta \; \mathcal{Q}(\theta, \theta_{\text{old}}) - \lambda \cdot \text{KL}(p_{\theta_{\text{old}}}(Z \mid \mathcal{Y}, \mathbf{X}{1:t}) \parallel p\theta(Z \mid \mathbf{X}{1:t})) - \epsilon \cdot \mathcal{L}{\text{ME}}$

实验

4.1 NuScenes（自动驾驶轨迹预测）

任务设置：

  • 输入：过去 2 秒内（2Hz 频率）ego-agent 的轨迹和周围车辆的历史轨迹 + 环境地图（鸟瞰图）。

  • 输出：预测未来 6 秒的轨迹。

实验设置：

  • 使用 AutoBot-Ego 模型，预测 ego-agent 的未来轨迹，设置 latent modes 数量为 c=10。latent mode指的是多种合理的未来情况

  • 训练使用单张 GTX 1080 Ti GPU，仅需约 3 小时。

评估指标：

指标名 含义
Min ADE (5)/(10) 前 5/10 个预测轨迹中，平均点对点 L2 距离的最小值。
Miss Rate Top-5/10 预测轨迹最大点误差超过 2m 的比例。
Min FDE (1) 最后一个点的预测误差。
Off Road Rate 预测轨迹偏离可通行道路的比例。

实验结果：

  • AutoBot-Ego (c=10) 在 Min ADE (10) 和 Off Road Rate 上取得最佳性能。

  • Ensemble（三模型集成）略有提升。

  • 与其他方法如 Trajectron++、WIMP 等相比，AutoBot-Ego 在准确性与效率上达到平衡。

4.2 Argoverse（城市交通轨迹预测）

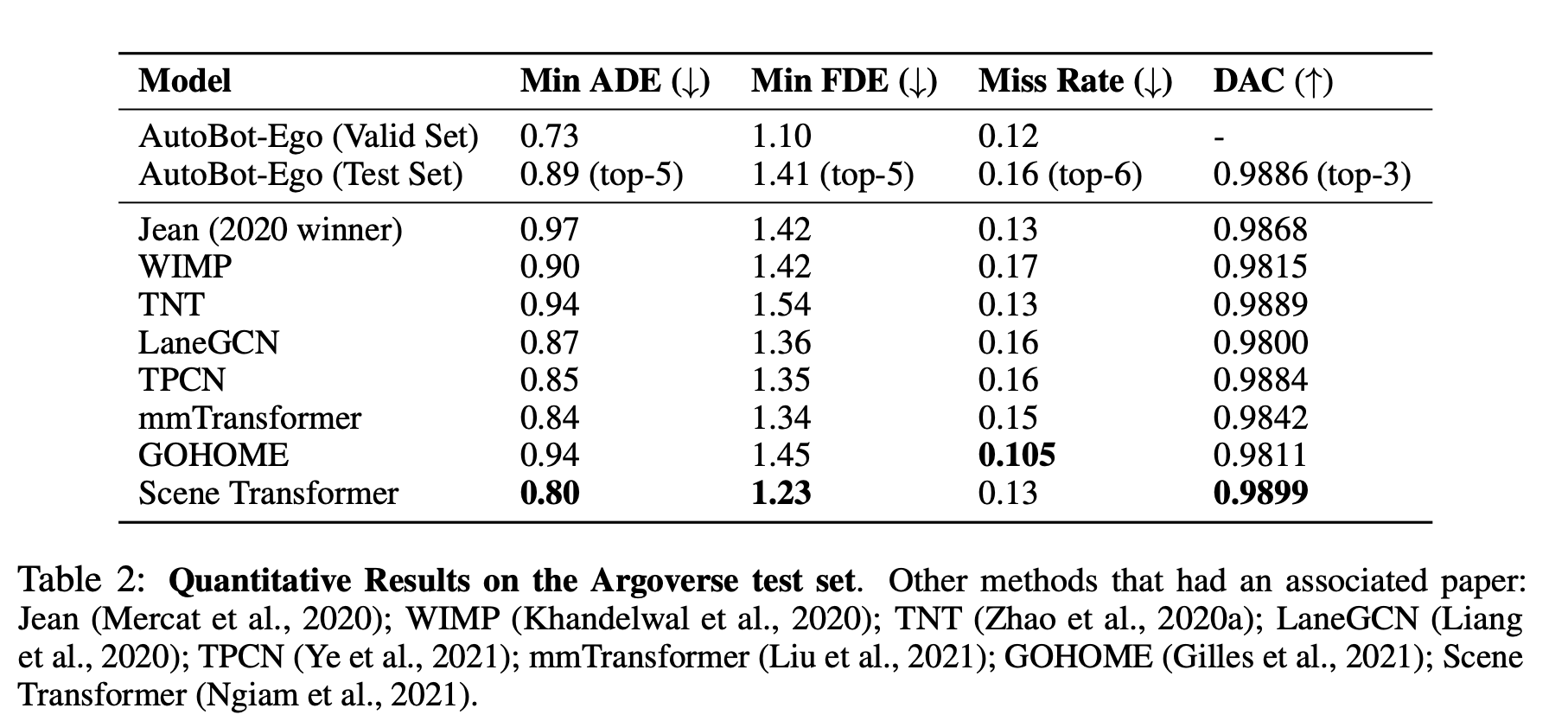
设置：

  • 预测车辆未来轨迹，AutoBot-Ego 设置为 c=6。

结果：

  • 虽然在部分指标上未超越顶尖方法（如 Scene Transformer），但模型计算量远小，训练时间仅为前沿方法的 0.4%。

  • 对比 2020 年冠军 Jean 模型，AutoBot-Ego 在 Min ADE 等指标上接近或优于其表现。

4.3 TrajNet++（多智能体预测与碰撞分析）

设置：

  • 输入：过去 9 帧的所有智能体轨迹。

  • 输出：未来 12 帧的所有智能体预测。

  • 使用 AutoBot 的完整多智能体版本，并进行消融实验。

比较模型：

  • Linear Extrapolation： 线性外推作为 baseline。

  • AutoBot-AntiSocial： 不使用 social attention 的版本。

  • AutoBot-Ego： 仅基于 ego-agent 预测。

  • AutoBot： 完整模型。

评估指标：

  • Ego-agent 的 Min ADE。

  • 多智能体之间的碰撞次数。

  • Scene-level Min ADE 和 FDE。

结果：

  • 完整的 AutoBot 模型显著减少碰撞次数（仅 139 次）并在 scene-level 准确度上优于其他变体。

  • 说明 social attention 的引入有助于更合理地建模 agent 间互动。

4.4 Omniglot（笔画序列生成任务）

任务设置：

  • Stroke Completion： 输入每个字符前半部分笔画，输出剩余部分。

  • Character Completion： 输入若干完整笔画，生成最后一个笔画。

模型比较：

  • 与 LSTM（带社会注意力机制）进行比较。

结果：

  • AutoBot 能生成更连贯、符合书写习惯的字符笔画，显示其在通用序列生成任务中的潜力。

  • 模型可泛化到非运动预测任务，说明其对集合序列建模的有效性。

Share: X (Twitter) Facebook LinkedIn